Lissage par transformation de Fourier

Une des définitions possible de la transformée de Fourier discrète est :

où NxN est la dimension de l'image f

La méthode est la suivante :

Transformation de Fourier de l'image f pour obtenir une information spectrale,
Filtrage dans l'espace de Fourier : multiplication du spectre par un filtre H(u,v),
Transformation de Fourier inverse.

Exemple :

                         Image de départ                                                             Image bruitée

          Information spectrale de l'image filtrée                                      Filtre H

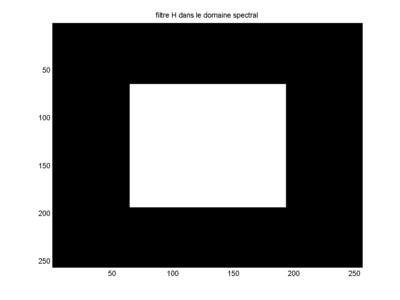
 Après multiplication l'information spectrale devient :                         Par TF inverse nous obtenons :

 A signaler que le filtre H ici est carrée ce qui n'est pas forcement une bonne chose c'est équivalent à convoluer dans l'espace image par la TF inverse du carrée soit un sinus cardinal. Cela aura un effet d'anneau dans l'image filtrée. Il est plus judicieux d'utiliser par exemple un filtre passe-bas de Butterworth. Pour le cas présent le bruit est blanc donc "pollue" toutes les fréquences. Le spectre du bruit et de l'image se supperposent donc le lissage enlève du bruit mais dégrade fortement l'image. Dans des cas particulier un filtrage plus sélectif est possible lorsque le bruit présent est périodique. Un exemple est la structure d'interférences parfois observée lorsque des équipements électromagnétiques fonctionnent près d'équipement video.

 Nous allons voir dans la page 4, le filtrage median qui respècte plus les contours.

Mis à zéro le 22/10/2004